Esperimenti, Retroprogramming

The decryption game

Claudio Parmigiani

Can an Apple-1 computer decipher a message encrypted with an Enigma cyphering machine in a reasonable time?

Recently I (re)watched the movie “The imitation game”: the English mathematical genius Alan Turing cracks the German Enigma code with help from fellow mathematicians, using an electro-mechanical device called Bombe.

At the end of the movie, I found myself wondering: “Would an Apple-1 be able to decrypt a text ciphered by an Enigma machine? If so, how fast would it be?”

The Enigma Machine is well documented in all its versions and variants, and the Internet is full of code and emulators.

I am not going to explain the operation principles of the Enigma Machine, on the Internet there is a plenty of valuable sources of knowledge. In the Bibliography section, you will find some link.

SEARCHING FOR… THE RIGHT CODE

What I was looking for was a short source code that could run in a few kiB of memory.

In this article, I will not go deep into the mathematical theories behind the “Enigma”, and I will not dwell on the different decryption techniques that could be used.

I found many programs, but unfortunately, many of them needed RAM that the Apple-1 simply does not have.

Finally, I found the source code candidate to be adapted for the CC65 cross compiler: http://www.cs.miami.edu/home/harald/enigma/

The small program can encrypt/decrypt messages with an user-defined machine setting or brute-force an encrypted message.

How does it work?

In the movie they use a word, called crib, they believe was encrypted in the message (i.e. “weather”) to program Turing’s Machine. The machine “simply” tries all the permutations of settings in order to obtain the original crib.

Due to the huge number of different initial settings of the Enigma machine, this method was very time consuming: many expedients were put into practice to reduce the number of permutations (i.e. the Diagonal Board method discovered by Turing’s colleague Gordon Welchman).

The program, written in C language, needed some adjustment to be compiled by CC65.

In this, I received invaluable help from Sergio Corpettini, who re-wrote extensive parts the code.

Thank you, Sergio! 🙂

Please note that the program must be compiled for the target system ‘replica1’, to override the 5 kiB limitation of the ‘apple1’ target. With this option, the compiler add four spurious bytes at the beginning of the code. Those bytes ($80, $02, $5C, $1F) have to be manually removed with an HEX editor, otherwise the program will not work on a real Replica / Original / Emulator.

When using an Emulator like Pom1, remember to keep all the 64 kiB addressable with CTRL E option. A ‘ram8k=0’ message will appear on to the terminal window.

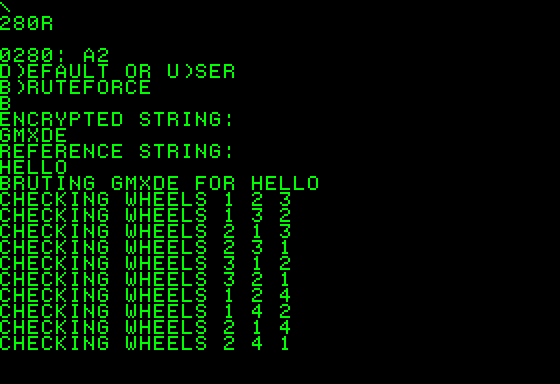
Using the program is quite simple: run it with 280R and then select the desired mode of operation (Brute-force).

It is then necessary to insert the encrypted message followed by the reference text (crib).

The program will then begin to test all the possible combinations.

If some combination give the crib as result, it will printed on the screen. If the crib is shorter than the encrypted message, there will be more candidate solutions.

Compared to a real Enigma Machine, please note that Rotor combination and Start position are printed in reverse order.

A FEW CONSIDERATIONS…

The original Apple-1s and Replicas, natively, have only 8 kiB of RAM, divided into two banks of 4 kiB, usually not contiguous (respectively: $0000-$0FFF and $E000-$EFFF).

By properly wiring the connections in the “Chip Select” area, it is possible to obtain a continuous segment of 8 kiB, starting at $0000 and ending at $1FFF.

Referring to the manual: the lowest usable address without disrupting the functionality of the computer is $0280.

Let’s do some math before warming up the soldering iron: $1FFF minus $0280 gives $1D7F Bytes of contiguous free memory, which is 7551 Bytes.

This is very close to what we need to run our program (8028 Bytes) but, unfortunately, it is not enough.

Nice try, anyway!

Could the program be optimized to run in only 7551 Bytes? Possibly.

Could the program be optimized to be faster, maybe using the Diagonal Board? Probably.

Could this optimization be done without exceeding the limit of 7551 Bytes? Probably not.

To overcome this problem and to run the program, I decided to use the built-in CFFA1’s RAM expansion, which increases the available contiguous memory to about 28 kiB.

A plenty of space!

In addition, I found other source codes (see bibliography) that would certainly be faster and more efficient, but unfortunately they need a lot of RAM and rely on external files.

Could these faster program run in 28 kiB of RAM ? Definitively not.

Another thing to keep in mind is that Turing’s Bombes were “programmed” with a completely different approach, based on so-called “loops”.

Also, there were many set of rotors spinning at the same time, in order to test different settings a sort of early parallel processing. The program I am going to use is more similar to a relentless steamroller, but way more fast than any electromechanical device (hopefully!).

Finally, at a certain point in the movie it seems that the Bombe gives back the key to decrypt a big amount of messages. This is not exactly true: all the candidate solutions were further analysed and tested by (human) cryptanalysts before being used to decipher real messages.

… AND LIMITATIONS

The decoding program has some limitations:

  • It emulates only one M3 machine, with three rotors chosen among the five available, plus a type “B” reflector.
  • The Steckerboard permutation/substitution is very time consuming. In the original C code, it was limited to the first five letters. In this version it has been skipped almost totally, limiting it to “A”, which means that Steckerboard plugs are not taken into account, at all.
  • Ring Setting is defaulted to AAA. To understand the reasons for this choice please refer to the reference article mentioned above.

RUN & RESULTS

The program runs perfectly on Originals and Replicas.

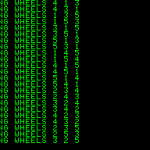After a few test on a real Replica, due to the high processing time, I decided to continue tests with the emulator Pom1.

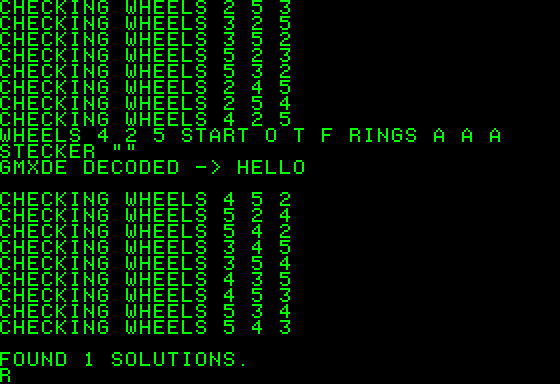
The benchmark has been done with a five-letter word (HELLO), encrypted by an emulator with:

  • Rotor “V” (5) in the leftmost position, Starting Position “F”, Ring position “A”
  • Rotor “II” (2) in the middle position, Starting Position “T”, Ring position “A”
  • Rotor “IV” (4) in the rightmost position, Starting position “O”, Ring position “A”
  • No Steckerboard plugs

After the encryption, the message HELLO become GMXDE.

The run time on a modern computer is almost instantaneous.

On an Apple-1, the processing time is about 7-8 minutes for each rotor combination.

By choosing three rotors from any of the five available, there are sixty possible rotor combinations. This brings the maximum processing time to about 420-480 minutes, or 7-8 hours.

Furthermore, the processing time gets a bit longer with longer messages/cribs.

FINAL COMMENTS

So, what is the answer to the question: “Can an Apple-1 computer decipher a message encrypted with an Enigma cyphering machine in a reasonable time?”

In my opinion, the answer should be: “Partly YES, but it is impractical”.

The main reason is: RAM constraints are inescapable, by design.

Moreover: only the “simplest” model of the Enigma Machine has been tested.

Due to the high processing times I have encountered, the most complex Enigma models have not even been taken into account.

An old-style coding (without using a compiler, or using a more efficient one) could save memory and increase speed but, frankly, these options are neither easy nor quick.

From the very beginning, this was just an experiment, with no practical potential.

It was, however, a nice journey to discover the limits of this little computer, making it do something, probably, for the first time ever.

If you want to try it by yourself, this is the C code:

/* enigma simulation and bombe, harald schmidl, april 1998
        the encoding scheme uses code from Fauzan Mirza's
        3 rotor German Enigma simulation
        source: http://www.cs.miami.edu/home/harald/enigma/  
  Modified: Sergio Corpettini to make it working with CC65 compiler and Apple-1 computer - 2019
  Edited: Claudio Parmigiani - 2019
*/

#include <stdio.h>
#include <string.h>
#include <ctype.h>

#define MSGLEN 80

//The following line define last steckerplug to be tested.
//i.e. 'D' will test substitutions from A to D.
//'A' to skip, to speed up.
#define TO 'A' 

char out[MSGLEN];

/* Rotor wirings */
char rotor[5][26]={
        /* Input "ABCDEFGHIJKLMNOPQRSTUVWXYZ" */
        /* 1: */ "EKMFLGDQVZNTOWYHXUSPAIBRCJ",
        /* 2: */ "AJDKSIRUXBLHWTMCQGZNPYFVOE",
        /* 3: */ "BDFHJLCPRTXVZNYEIWGAKMUSQO",
        /* 4: */ "ESOVPZJAYQUIRHXLNFTGKDCMWB",
        /* 5: */ "VZBRGITYUPSDNHLXAWMJQOFECK" };
char ref[26]="YRUHQSLDPXNGOKMIEBFZCWVJAT";

char notch[5]="QEVJZ";

/* Encryption parameters follow */

typedef struct P
{
        char order[3];/*={ 1, 2, 3 };*/
        char rings[3];/*={ 'A','A','A' };*/
        char pos[3];/*={ 'A','A','A' };*/
        char plug[10];/*="AMTE";*/
} Params;

/*take a char and return its encoded version according to the
        encryption params, update params, i.e. advance wheels
        this part uses Fauzan Mirza's code*/
char scramble(char c, Params *p)
{
        int i, j, flag = 0;

                c=toupper(c);
                if (!isalpha(c))
                        return -1;
                /* Step up first rotor */
                p->pos[0]++;
                if (p->pos[0]>'Z')
                        p->pos[0] -= 26;

                /* Check if second rotor reached notch last time */
                if (flag)
                {
                        /* Step up both second and third rotors */
                        p->pos[1]++;
                        if (p->pos[1]>'Z')
                                p->pos[1] -= 26;
                        p->pos[2]++;
                        if (p->pos[2]>'Z')
                                p->pos[2] -= 26;
                        flag=0;
                }

                /*  Step up second rotor if first rotor reached notch */
                if (p->pos[0]==notch[p->order[0]-1])
                {
                        p->pos[1]++;
                        if (p->pos[1]>'Z')
                                p->pos[1] -= 26;
                        /* Set flag if second rotor reached notch */
                        if (p->pos[1]==notch[p->order[1]-1])
                                flag=1;
                }

                /*  Swap pairs of letters on the plugboard */
                for (i=0; p->plug[i]; i+=2)
                {
                        if (c==p->plug[i])
                                c=p->plug[i+1];
                        else if (c==p->plug[i+1])
                                c=p->plug[i];
                }

                /*  Rotors (forward) */
                for (i=0; i<3; i++)
                {
                        c += p->pos[i]-'A';
                        if (c>'Z')
                                c -= 26;

                        c -= p->rings[i]-'A';
                        if (c<'A')
                                c += 26;

                        c=rotor[p->order[i]-1][c-'A'];

                        c += p->rings[i]-'A';
                        if (c>'Z')
                                c -= 26;

                        c -= p->pos[i]-'A';
                        if (c<'A')
                                c += 26;
                }

                /*  Reflecting rotor */
                c=ref[c-'A'];

                /*  Rotors (reverse) */
                for (i=3; i; i--)
                {
                        c += p->pos[i-1]-'A';
                        if (c>'Z')
                                c -= 26;

                        c -= p->rings[i-1]-'A';
                        if (c<'A')
                                c += 26;

                        for (j=0; j<26; j++)
                                if (rotor[p->order[i-1]-1][j]==c)
                                        break;
                        c=j+'A';

                        c += p->rings[i-1]-'A';
                        if (c>'Z')
                                c -= 26;

                        c -= p->pos[i-1]-'A';
                        if (c<'A')
                                c += 26;
                }

                /*  Plugboard */
                for (i=0; p->plug[i]; i+=2)
                {
                        if (c==p->plug[i])
                                c=p->plug[i+1];
                        else if (c==p->plug[i+1])
                                c=p->plug[i];
                }

        return c;
}

/*take a string, return encoded string*/
char *enigma(char *in, Params *p)
{
        int j;
        for(j = 0; j < strlen(in); j++){
         //printf("scramble in enigma func

        out[j] = scramble(in[j], p);
        }
        out[j] = '\0';

        return out;
}

/*read in a string, and pass it through enigma*/
void cypher(Params *p)
{
        char in[MSGLEN], s[MSGLEN];
        int c, i = 0;

        while((c = getchar()) != '\n')
        {
                in[i] = toupper(c);
                i++;
        }
        in[i] = '\0';
        strcpy(s, enigma(in, p));
        printf("\
}

/*given a cipher text, and a crib, test all possible settings of wheel order a, b, c*/
void rotate(int a, int b, int c, char *cyph, char *crib, char *plug, int *ct)
{
        int i;
        Params p;
        Params cp;
        p.order[0] = a;
        p.order[1] = b;
        p.order[2] = c;
        p.rings[0] = 65;
        p.rings[1] = 65;
        p.rings[2] = 65;
        strcpy(p.plug, plug);
        for(p.pos[0] = 65; p.pos[0] <= 90; p.pos[0]++)
        {

                for(p.pos[1] = 65; p.pos[1] <= 90; p.pos[1]++)
                {
                        for(p.pos[2] = 65; p.pos[2] <= 90; p.pos[2]++)
                        {
                        //printf("
/*        for(p.rings[0] = 'A'; p.rings[0] <= 'Z'; p.rings[0]++)
                                {
                                        for(p.rings[1] = 'A'; p.rings[1] <= 'Z'; p.rings[1]++)
                                        {
                                                for(p.rings[2] = 'A'; p.rings[2] <= 'Z'; p.rings[2]++)
                                                {
*/            //Params cp = p;
                        memcpy((void *)&cp,(void *)&p,sizeof(p));
                        i = 0;

                        while(strlen(crib) > i)
                        {
                                if(cyph[i] != scramble(crib[i], &cp))
                                break;
                        else
                                i++;
                        }
                        if(strlen(crib) == i)
                        {
                        char s[MSGLEN];

                        (*ct)++;
                        printf("Wheels
                                                                                                p.order[0], p.order[1], p.order[2],
                                                                                                p.pos[0], p.pos[1], p.pos[2],
                                                                                                p.rings[0], p.rings[1], p.rings[2], p.plug);
                        cp = p;
                        strcpy(s, enigma(cyph, &cp));
                                                                printf(
                                                        }
/*            }
                                        }
                                }
*/      }
                }
        }
}

/*do the whole check including steckering of up to two pairs of letters*/
void test(int a, int b, int c, char *cyph, char *crib, int *ct)
{
        char A, B, C, D;
        int i = 0;
        int cs = 0;
        char s[5];

        strcpy(s, "");
        printf("Checking wheels
        for(cs = 0; cs < 3; cs++)
        {
                if(cs > 0)
                {
                        for(A = 'A'; A <= TO; A++)
                        {
                                for(B = A + 1; B <= TO; B++)
                                {
          s[0] = A;
          s[1] = B;
          s[2] = '\0';
          if(cs > 1)
          {
            for(C = A + 1; C <= TO; C++)
            {
              if(C == B)
              continue;
              for(D = C + 1; D <= TO; D++)
                                                        {
                if(D == A || D == B)
                continue;
                i++;
                s[2] = C;
                s[3] = D;
                s[4] = '\0';
                                        rotate(a, b, c, cyph, crib, s, ct);
              }
                                                }
                                        }
          else
          rotate(a, b, c, cyph, crib, s, ct);
                                }
                        }
                }
                else
                rotate(a, b, c, cyph, crib, s, ct);
        }
}


/*run on all permutations of wheels a, b, c*/
void permute(int a, int b, int c, char *cyph, char *crib, int *ct)
{
        test(a, b, c, cyph, crib, ct);
        test(a, c, b, cyph, crib, ct);
        test(b, a, c, cyph, crib, ct);
        test(b, c, a, cyph, crib, ct);
        test(c, a, b, cyph, crib, ct);
        test(c, b, a, cyph, crib, ct);
}

/*all triples of five possible wheels*/
void permuteAll(char *cyph, char *crib)
{
        int ct = 0;
        printf("bruting
        permute(1, 2, 3, cyph, crib, &ct);
        permute(1, 2, 4, cyph, crib, &ct);
        permute(1, 2, 5, cyph, crib, &ct);
        permute(1, 3, 4, cyph, crib, &ct);
        permute(1, 3, 5, cyph, crib, &ct);
        permute(1, 4, 5, cyph, crib, &ct);
        permute(2, 3, 4, cyph, crib, &ct);
        permute(2, 3, 5, cyph, crib, &ct);
        permute(2, 4, 5, cyph, crib, &ct);
        permute(3, 4, 5, cyph, crib, &ct);
        printf("\nFound
}

/*helper to read a character*/
char readCh()
{
        char c, ret;

        while((c = getchar()) != '\n')
        ret = c;
        return ret;
}

/*init the starting position*/
void initParams(Params *p)
{
        int i;
        char c;
        char cyp[64] = "";
        char ref[64] = "";

  printf("\n");
        printf("d)efault or u)ser \n");
        printf("b)ruteforce\n");

        c = readCh();
        if(c == 'B')
        {
                printf("Encrypted string: \n");
                //fgets(cyp,128,stdin);
                i=0;
                while((c = getchar()) != '\n'){
                cyp[i] = c;
                i++;
                }
                printf("Reference string: \n");
                i=0;
                while((c = getchar()) != '\n'){
                ref[i] = c;
                i++;
                }

                permuteAll(cyp, ref);
                return;

        }
        if(c != 'U')
        {
                for(i = 0; i < 3; i++)
                {
                        p->order[i] = i + 1;
                        p->rings[i] = 'A';
                        p->pos[i] = 'A';
                }
                strcpy(p->plug, "");
        }
        else
        {
                        for(i = 0; i < 3; i++)
                        {
                                printf("Wheel
                                p->order[i] = readCh() - 48;
                        }
                        for(i = 0; i < 3; i++)
                        {
//        printf("Ring 
                                p->rings[i] = 'A';/*readCh();*/
                        }
                        for(i = 0; i < 3; i++)
                        {
                                printf("Start
                                p->pos[i] = readCh();
                        }
                        printf("Stecker: ");
                        i = 0;
                        while((c = getchar()) != '\n')
                        {
                                p->plug[i] = c;
        i++;
                        }
                        p->plug[i] = '\0';
        }
        printf("Wheels
                                 p->order[0], p->order[1], p->order[2],
                                 p->pos[0], p->pos[1], p->pos[2],
                                 p->rings[0], p->rings[1], p->rings[2], p->plug);
}


/********************************************MAIN*********************************************/
void main()
{
        Params p;
        initParams(&p);
        cypher(&p);
}

It can run on a modern computer as well after being compiled with gcc.

Here follows the program compiled for Apple-1 (run with 280R): enigma.bin

This is the same program compiled for Apple-1 in WOZ Monitor format (run with 280R):enigma.mon

CREDITS

Many thanks to Sergio Corpettini for his tireless work of revising the source code.

BIBLIOGRAPY / SOURCES

Have your say